C# Programming > Math

C# Quadratic Formula Solver

 

Quadratic Equation

Implementing the quadratic formula in C# allows .NET programs to quickly and easily solve quadratic equations. The applications for solving quadratic equations are up to the developer.

.NET Implementation

First we will implement the straight-forward quadratic formula:

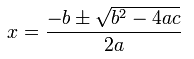
Remember that the quadratic formula gives up to two answers. This makes sense since the formula is solving for the values of x in which a parabola crosses the x-axis. If the parabola starts above (or below) the x-axis then there will be no answers. If the parabola touches the x-axis at exactly the bottom (or top, depending on the direction) then there will be exactly one answer. If each of the parabola's "arms" cross the x-axis then there will be two answers.

If there are two results, how can we write a C# function to return both solutions? The trick is to use the out parameter passing mode. The function itself will not return a value. Instead, we will pass to the function two empty variables that will each be assigned a computed solution.

Here is the code, which is not too difficult to understand:

public static void SolveQuadratic(double a, double b, double c, out double x1, out double x2)
{
    //Quadratic Formula: x = (-b +- sqrt(b^2 - 4ac)) / 2a

    //Calculate the inside of the square root
    double insideSquareRoot = (b * b) - 4 * a * c;

    if (insideSquareRoot < 0)
    {
        //There is no solution
        x1 = double.NaN;
        x2 = double.NaN;
    }
    else
    {
        //Compute the value of each x
        //if there is only one solution, both x's will be the same
        double sqrt = Math.Sqrt(insideSquareRoot);
        x1 = (-b + sqrt) / (2 * a);
        x2 = (-b - sqrt) / (2 * a);
    }
}

Notice that we can quickly tell if there is no solution by calculating the inside portion of the square root (the discriminant). If the discriminant is negative then there is not real number solution.

Floating Point Implementation

The above C# algorithm will work just fine because it uses double primitives. However if we wanted to use float primitives, we might start to get inaccurate results due to loss of significance.

To avoid this problem, we can compute the formula is a slightly different way to achieve more accurate results.

The C# implementation is very similar:

public static void SolveQuadratic(float a, float b, float c, out float x1, out float x2)
{
    //Calculate the inside of the square root
    float insideSquareRoot = (b * b) - 4 * a * c;

    if (insideSquareRoot < 0)
    {
        //There is no solution
        x1 = float.NaN;
        x2 = float.NaN;
    }
    else
    {
        //Compute the value of each x
        //if there is only one solution, both x's will be the same
        float t = (float)(-0.5f * (b + Math.Sign(b) * Math.Sqrt(insideSquareRoot)));
        x1 = c / t;
        x2 = t / a;
    }
}

Overloading in .NET allows us to have both C# functions in the same class, letting the compiler call the appropriate one when working with doubles or floats.

Quadratic Equation Solver

Download below the quadratic equation solver written in C#. It lets you compare the results between using double and float types.

Back to C# Article List